Webページのデザインについて

最近Webページの記事が増えてきた。
が、私はフレームというものが嫌いだ。
なのでそういうものを使ってこなかった。
しかし、かといって読者がページ内を移動するのに必要なナビゲーションがなくていい、
というわけにはいかなくなってきた。

近いうちに、Webページ全体になんらかのナビゲーション的なものを付け加える大工事をしなければ・・・

数学の記事を書いてみたが

本家Webページに数学の記事を書いてみた。

http://sammaya.garyoutensei.com/math_phys/math1/index.html

最終目標は四元数とパウリ行列の関係なのだが、
そこに行く前にいままで引っかかっていた実数の完備性やら
複素数の性質についても触れておきたい思い、ちょっと遠回りしながら書いてみようと思う。

長らく、パウリ行列というのはどういう代数のもとで出てくるか、疑問だった。
３次元での回転と関係していそうなのに、2次（あるいは４次）の行列になっているのはなぜか。
その辺の疑問と、ディラック方程式の因数分解として４次元のスピノールが出てくるあたりの議論との関連。
そのようなことを考えていたときにふと目に留まった文章がある。



（はじめてAmazonアフィリエイトを使ってみたｗ）
ここでのヤコービの章とハミルトンの章。
因数分解の問題から四元数にいたる過程の話から、
ディラック方程式からパウリ行列が出てくることの類似性について気づいた。
そして調べてみると、パウリ行列は四元数の１つの表現になっている。
ここだけを書いてしまえばおそらくそんな多い分量にはならないだろう。
しかし、そこに至る思考過程には数学や物理学で重要な概念が含まれているように思う。
そのあたりを気づく限り抽出しつつ、文章を書いていきたいと思う。

LaTeX2HTMLを使ってみる

WEBサイトの文章にどうしても数式を使いたいというとき、
HTMLで数式を書こうというのはかなり大変です。

そこで、TeXで文章を作成し、それが自動でHTMLになったらどんなに楽なことでしょう。
TeXでソースを書いておけば、PDF形式で配布することもできますし、
可読性もぐっとあがるはずです。

そこで、LaTeX2HTMLというものをつかってみました。

Visual C++のrand()関数でベクトルを生成してはまる

久しぶりにホームページのプログラム系記事をUPしました。
モンテ・カルロ法による水素原子の電子軌道

さて、ここでrand()でベクトルを生成すると、特定の平面の点が生成されません。



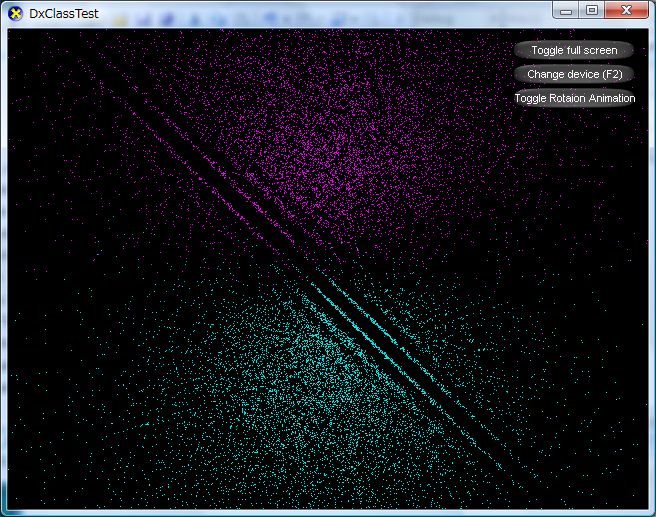
このように線が入ったような見え方になります。
しばらくこの原因が分かりませんでした。
最初、確率計算や表示系のバグかとおもっていましたが、
どうやらそうではないらしいと。
で、話にはきいていた乱数の問題を疑い、自前で乱数クラスをつくってやってみました。



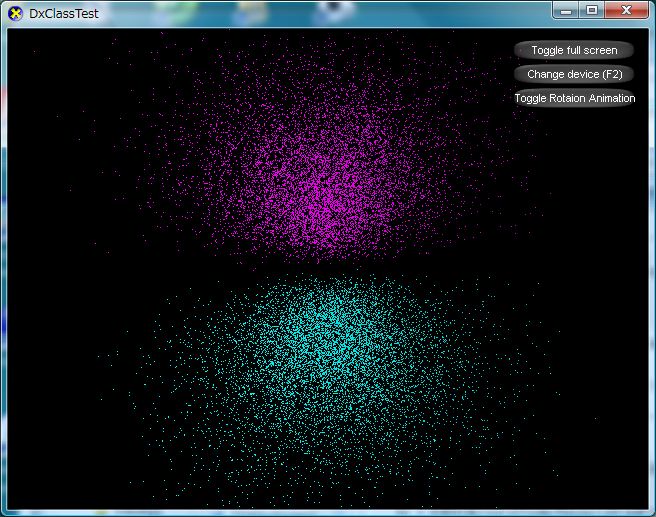
するとすっきり筋はきえてしまいました・・・
こんなにはっきり出るとは思いませんでした。

ここで使用した方法は、足し算法です。

VAIO type ZでCUDA2.3を使う

最近、ゲームにかまけてプログラミングをしてませんでした。

さて、CUDA2.3が使えるtypeZ用のドライバがでているようです。

まずドライバをダウンロードしてきます。
http://forum.notebookreview.com/showpost.php?p=5093917&postcount=460

例によって登録が必要です。
以前のものをいれたことがある方は、ログインできると思います。

手順ですが、ほかのサイトなどで紹介されていた方法と、私の環境では違ったので
（VGN-Z90Sでのインストール)書いておきます。

０．まず上記サイトからのファイルを適当なフォルダに解凍しておきます

１．デバイスマネージャから２つのディスプレイドライバを削除する

２．再起動

３．再起動するとOSが自動で標準ドライバをいれてしまう

４．ここで「ドライバの更新」をしても「最新です」とかいわれてしまうので、
解凍したフォルダからsetup.exeを直接起動。

５．インストール開始

６．再起動後、ToolkitとSDKをインストール

これでCUDA2.3が動いています。

とりあえず報告まで。

参照させていただいた記事をトラックバックしておきます。
http://kgxpx834.blog58.fc2.com/blog-entry-9.html